Those who know me will tell you that I am an incurable romantic, and also that I have a soft spot for mathematical puzzles and games. Here are some mathematical odds and ends that I have found to be unusually romantic - see what you think. Follow the links on the titles for further information.
The Happy End Problem
The Happy End Problem is so named because two of the mathematicians who met whilst working on the problem, E. Klein and G. Szekeres, got married and lived happily ever.
Suppose you have g>=3 points on the plane, no three of which are collinear.
For some arrangements of the g points, you will be able to pick n of them to make a convex n-sided polygon. For example, for n=3 you will always be able to make a convex triangle because all triangles are convex and no 3 points are collinear.
For n=4, g=4 does not suffice because the four points could be arranged as the corners of a triangle and a fourth point inside the triangle - no convex quadrilateral can be obtained from these points, but g=5 does (see figure 1).
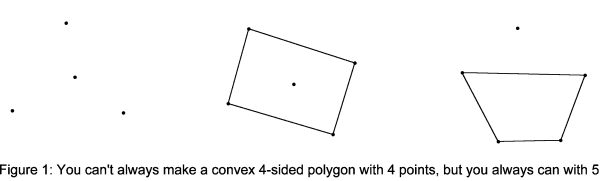
The problem is to determine the number of points g(n) you need to make an n-sided polygon no matter where the points are (as long no 3 of them are collinear).
The first few values of g(n) are:
g(3)=3
g(4)=5
g(5)=9
g(6)=17
Higher values are unknown, but at most the values of A052473:
g(7)<=128
g(8)<=464
g(9)<=1718
(Thanks to fjh for the correction.)
Mrs Miniver's Problem
According to Mrs Miniver, in the ideal romance each lover shares exactly two thirds of their interests with the other. She wishes to symbolize this with a diagram of two circles of the same size, overlapping such that the area of the overlap is that same as sum of the areas of each of the two crescents formed (half of the area of the overall figure). What is the ratio of the distance between the centres of the circles and their radii?
The answer is approximately 0.529864, and is believed to be trancendental.
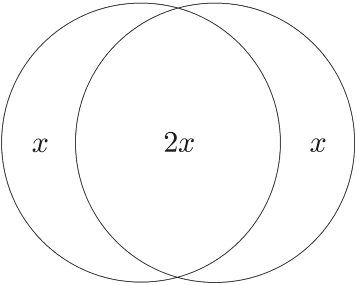
(An earlier version of the problem stated here was to find the answer if the intersection area was the same as the area of one of the crescents, which gives the answer 0.807946, but this isn't what Mrs Miniver originally stated as the ideal romance).
Happy numbers
Pick a positive integer n. Take the squares of the digits and add them up. Repeat. If you eventually get to 1, n is happy. If you don't, n is unhappy. The first few happy numbers in base 10 are 1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100.
Friendly numbers
Two postive integers a and b are friendly if the sum of the proper factors of a is b and the sum of the proper factors of b is a.
Happy friendly numbers
Here's a romantic puzzle: in which bases (if any) can you find a pair of numbers which are friendly with each other and happy together?
The Kissing problem
An interesting article about kissing spheres.