When I learned about General Relativity at university I sometimes used to wonder if there was a metric in which this object could exist:
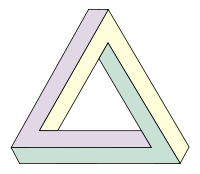
And be what it appears to be, i.e. the straight lines are (lightlike) geodesics and the corners are (locally) right-angles.
Initially, I imagined that such a metric might be possible without any sort of topological defect. In particular, while the triangle would look like the picture above when viewed "face on" it would appear to curve as you moved around it and examined it from different angles. While lightlike geodesics always look straight when you look along them from a point on the geodesic, they can still look curved when viewed externally. The photon sphere around a black hole is an example of a set of such geodesics thought to occur in our universe.
Thinking about it some more, I suspect something strange is going to have to happen in the middle of the triangle - if you try to shrink the triangle to a point, what happens?
Imagine being in this universe and travelling all the way around the triangle. I think that upon doing so, one would find that one had actually only turned through 270 degrees instead of the full 360 (and would also have rotated about the axis of travel). I suspect that this means that such a metric would have to have a topological defect (a cosmic string) passing through the center of the triangle. This would cause a discontinuity when viewing the triangle, so one would not be able to see the entire illusion in all its glory as it is shown above.